Di aljabar, penjumlahan dua suku, seperti a + b, disebut binomial. Teorema binomial memberikan bentuk ekspansi dari pangkat binomial (a + b)n, untuk setiap n bilangan bulat tidak negatif dan semua bilangan real a dan b.
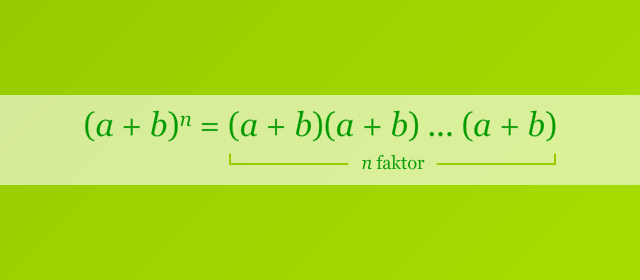
Perhatikan apa yang terjadi ketika kita menghitung beberapa pangkat yang pertama dari a + b. Berdasarkan sifat distributif, kita mendapatkan bahwa pangkat dari a + b merupakan penjumlahan dari suku-suku yang berupa kombinasi perkalian dari a dan b. Perhatikan ilustrasi berikut.
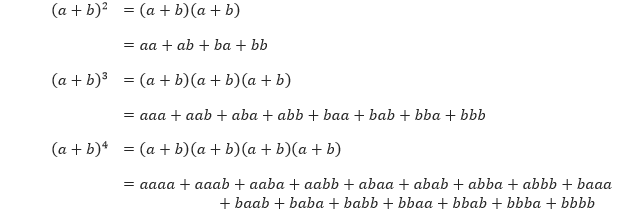
Sekarang perhatikan ekspansi dari (a + b)4. Suku-suku dari ekspansi ini diperoleh dengan mengalikan satu dari dua suku faktor pertama dengan satu dari dua suku faktor kedua dengan satu dari dua suku faktor ketiga dan dengan satu dari dua suku faktor keempat. Sebagai contoh, suku abab diperoleh dengan mengalikan suku-suku a dan b yang ditandai dengan tanda panah.
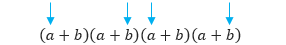
Karena ada dua kemungkinan a dan b dari setiap suku yang dipilih pada 1 dari 4 faktor suku-suku ekspansi binomial, maka akan ada 24 = 16 suku ekspansi (a + b)4.
Selanjutnya, suku-suku serupa, yaitu suku-suku yang memiliki faktor a dan b sama banyak dapat dikombinasikan karena perkalian bersifat komutatif. Tetapi kita perlu mengetahui banyaknya masing-masing suku yang serupa tersebut. Sebagai contoh kita akan menentukan banyaknya suku yang terdiri dari tiga a dan satu b. Untuk menentukan banyaknya suku ini sama dengan menentukan banyaknya cara kita mengambil 1 bilangan 1 sampai 4 sebagai nomor urut dari faktor b. Salah satu contohnya kita mungkin mendapat bilangan 3 yang merepresentasikan aaba (3 merupakan nomor urut dari b, sedangkan sisanya menjadi nomor urut a). Contoh lain, kita mungkin mendapat bilangan 1 yang merepresentasikan baaa. Sehingga banyaknya suku yang terdiri dari tiga a dan satu b adalah kombinasi 1 dari 4 yaitu 4. Semua suku yang terdiri dari tiga a dan satu b adalah aaab, aaba, abaa, dan baaa.
Berdasarkan sifat komutatif dan asosiatif perkalian, keempat suku tersebut memiliki nilai yang sama dengan a3b. Karena suku-suku yang sama dengan a3b berjumlah 4, maka koefisien dari a3b adalah 4, yang diperoleh dari kombinasi 1 (pangkat dari salah satu faktor a3b, yaitu b) dari 4 (jumlah pangkat dari semua faktor a3b).
Dengan cara yang sama, kita akan mendapat 6 (diperoleh dari kombinasi 2 dari 4) suku yang terdiri dari dua a dan dua b, yaitu aabb, abab, abba, baab, baba, dan bbaa. Sehingga koefisien dari suku a2b2 adalah 6. Cara ini juga berlaku untuk menentukan koefisien dari suku-suku ekspansi (a + b)4 lainnya.
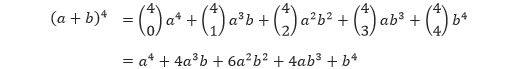
Teorema binomial menggeneralisasi rumus di atas untuk sembarang pangkat n bilangan bulat tidak negatif.
Teorema Binomial
Diberikan sembarang bilangan real a dan b, serta bilangan bulat tidak negatif n,
Perhatikan bahwa bentuk kedua dan pertama pada persamaan di atas adalah sama, karena kombinasi 0 dari n sama dengan satu, demikian juga dengan kombinasi n dari n. Untuk lebih memahami mengenai penggunaan teorema binomial dalam pemecahan masalah, perhatikan contoh berikut.
Contoh: Penggunaan Teorema Binomial dalam Pemecahan Masalah
Dengan menggunakan teorema binomial, tunjukkan bahwa
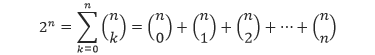
untuk semua bilangan bulat n ≥ 0.
Pembahasan Karena 2 = 1 + 1, maka 2n = (1 + 1)n. Dengan menerapkan teorema binomial dengan a = 1 dan b = 1, diperoleh
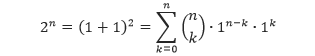
Karena 1n – k = 1 dan 1k = 1. Akibatnya,
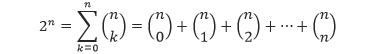
Apabila diperhatikan, rumus di atas sama dengan banyaknya semua himpunan bagian dari himpunan yang memiliki n anggota/elemen, karena setiap himpunan bagian tersebut terdiri dari kombinasi 0, 1, 2, …, n dari n yang merupakan banyaknya anggota dari himpunan tersebut.

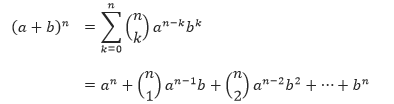
0 Response to "Theorema Binomial Matematika Diskrit"
Post a Comment