Garis Istimewa Pada Segitiga

1) Garis Berat
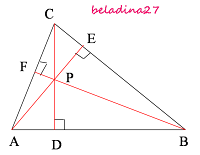
Garis berat adalah ruas garis yang ditarik dari sebuah titik sudut segitiga dan membagi sisi dihadapannya menjadi dua sama panjang.

Garis-garis beratnya adalah AD, BE, CF. Titik potong ketiga garis beratnya disebut titik berat (titik P).

Teorema 1
Garis-garis berat dalam segitiga berpotongan atas bagian yang perbandingannya 2 : 1.
AP : PD = BP : PE = CP : PF = 2 : 1

Bukti:
Hubungkan D dan E maka DE//AB.
Karena D dan E berturut-turut adalah titik tengah BC dan AC, maka DE = 1/2 AB (AB : DE = 2 : 1).
Lihat  dan .
             (sudut dalam berseberangan)
             (sudut bertolak belakang)
        (sebangun)
Jadi, AP : PD = BP : PE = CP : PF = 2 : 1   (terbukti).

Teorema 2
Jika , ,  berturut-turut adalah garis berat ke sisi a, b, c maka
     
     
     

Bukti:
Menurut teorema Stewart,
     
   
                       (terbukti)


2) Garis Bagi
Garis bagi adalah ruas garis yang ditarik dari sebuah titik sudut segitiga dan membagi sudut menjadi dua sama besar.

Garis-garis baginya adalah AF, BD, CE. Titik potong ketiga garis baginya disebut titik bagi (titik P).

Teorema 1

Garis yang membagi sisi didepannya menjadi dua bagian yang berbanding seperti sisi-sisi yang berdekatan.
p : q = b : a





Bukti:
Lihat  dan .
            (sudut dari garis bagi)
                          (berhimpit)
             (jelas)
        (kongruen)

Tarik garis  dan , maka DE = DF  ().
Lihat  dan .
        
                                                                   

        (ii) Jika garis tinggi dari titik C adalah   (CD).
             
                                                                    
Jadi, 
             (terbukti)

Teorema 2

Kuadrat garis bagi dalam sama dengan hasil kali sisi sebelah dikurangi hasil kali bagian sisi dihadapannya.







Bukti:
CD adalah garis bagi, maka a : b = q : p atau ap = bq.
Menurut teorema Stewart,
        
        
        
        
        
        
                      (terbukti)

3) Garis Tinggi
Garis tinggi adalah ruas garis yang ditarik dari sebuah titik sudut segitiga dan tegak lurus dengan sisi dihadapannya.

Garis-garis tingginya adalah AE, BF, CD. Titik potong ketiga garis tingginya disebut titik tinggi (titik P).

Teorema 1

Dua garis tinggi dalam segitiga berbanding terbalik dengan sisinya.
 







Bukti:



Sehingga diperoleh,
          
                
                         (terbukti)

Teorema 2
Jika diketahui ,  dan , ,  berturut-turut adalah garis tinggi pada sisi a, b, c maka
        

        

        

Bukti:
(menunggu update yaa ^_^ . . . . aku capek ngetiknyaaaaa)

4) Garis Sumbu
Garis sumbu adalah ruas garis yang membagi sisi segitiga menjadi dua bagian sama panjang dan tegak lurus pada sisi tersebut.

Garis-garis sumbunya adalah k, l, dan m. Titik potong ketiga garis sumbunya disebut titik sumbu (titik P).


sumber : beladina27

Tweet