Integral Parsial - Kalkulus

Teknik integral parsial dapat diterapkan dalam berbagai macam fungsi, dan secara khusus teknik tersebut sangat berguna ketika dijumpai integran yang melibatkan perkalian fungsi-fungsi aljabar dan transendental. Sebagai contoh, integral parsial akan sangat berfungsi dengan baik untuk menyelesaikan,

Integral parsial didasarkan pada rumus turunan dari perkalian dua fungsi.

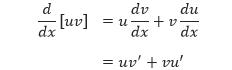
di mana u dan v adalah fungsi-fungsi yang terdiferensialkan dalam x. Jika u’ dan v’ kontinu, kita dapat mengintegralkan kedua ruas dari persamaan di atas dan memperoleh

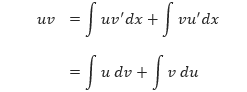
Dengan menulis kembali persamaan di atas, diperoleh teorema berikut.

Teorema 1: Integral Parsial
Jika u dan v adalah fungsi-fungsi dalam x yang kontinu dan terdiferensialkan, maka

Rumus integral parsial ini menyatakan integral aslinya ke dalam bentuk integral yang lain. Berdasarkan pemilihan u dan dv, akan lebih mudah menyelesaikan bentuk integral yang kedua daripada bentuk aslinya. Karena pemilihan u dan dv sangatlah krusial dalam proses integral parsial, berikut ini panduan dalam memilih u dan dv.

---

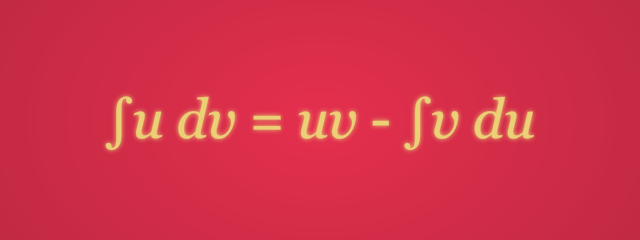
Panduan dalam Proses Integral Parsial

1. Cobalah untuk memisalkan dv sebagai bagian yang sangat rumit dari integran yang sesuai dengan aturan dasar integral. Sehingga u merupakan faktor lainnya dari integran.
2. Cobalah untuk memisalkan u sebagai bagian dari integran yang turunannya lebih sederhana dari u. Selanjutnya dv merupakan faktor integral lainnya.

Perhatikan bahwa dv selalu memuat dx dari integran aslinya.

---

Untuk lebih memahami bagaimana menyelesaikan permasalahan integral dengan menggunakan metode integral parsial, perhatikan beberapa contoh berikut.

Contoh 1: Integral Parsial

Tentukan,

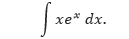
Pembahasan Untuk menerapkan integral parsial, kita perlu untuk menuliskan integral tersebut ke dalam

Terdapat beberapa cara untuk melakukan hal tersebut, yaitu

Panduan dalam pemilihan u dan dv sebelumnya menyarankan kita untuk memilih pilihan pertama karena turunan dari u = x lebih sederhana dari x, dan dv = e^x merupakan bagian yang paling rumit dari integran yang sesuai dengan aturan dasar integral.

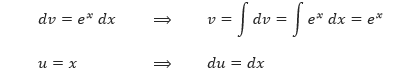
Sekarang, dengan integral parsial akan dihasilkan

Untuk memeriksa hasil pengintegralan ini, kita dapat menurunkan hasil tersebut untuk mendapatkan integran aslinya.

Catatan Pada contoh 1 di atas kita tidak perlu menuliskan konstanta ketika menyelesaikan

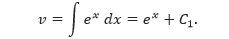
Untuk mengilustrasikan hal ini, cobalah mengganti v = e^x dengan v = e^x + C₁ kemudian terapkan proses integral parsial untuk melihat bahwa kamu akan mendapatkan hasil yang sama.

Tweet