TABUNG, KERUCUT, DAN BOLA
 |
| Tabung - Kerucut - Bola |
TABUNG
Tabung adalah prisma yang bidang alas dan tutupnya berbentuk lingkaran. Perhatikan unsur-unsur tabung pada gambar di bawah ini.
 |
| Tabung |
Keterangan
t = tinggi tabung
r = jari-jari tabung
KERUCUT
Kerucut adalah limas yang bidang alasnya berbentuk lingkaran. Unsur-unsur kerucut dapat dilihat pada gambar di bawah ini.
 |
| Kerucut |
Keterangan :
t = tinggi kerucut
r = jari-jari kerucut
s = garis pelukis
(Garis Pelukis yaitu gari yang menghubungkan titik puncak kerucut dengan titik pada keliling sisi alas kerucut).
BOLA
Bola merupakan satu-satunya bangun ruang yang hanya tersusun atas satu bidang sisi. Bidang sisi tersebut berupa bidang sisi lengkung. Unsur-unsur bola yang terlihat seperti gambar di bawah ini.
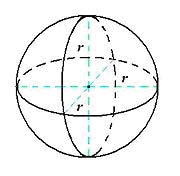 |
| Bola |
Keterangan :
r = jari-jari bola
LUAS DAN VOLUME BANGUN RUANG SISI LENGKUNG
TABUNG
Luas Selimut = keliling alas x tinggi
 |
| Luas Selimut Tabung |
Luas Tabung = Luas alas + Luas tutup + luas selimut
 |
| Luas Tabung |
Volume Tabung = Luas alas x tinggi
 |
| Volume Tabung |
KERUCUT
 |
| Kerucut |
Luas Juring
 |
| Luas Juring |
Luas Selimut = Luas Juring, maka :
 |
| Luas Selimut |
Luas Kerucut = Luas selimut + luas alas
 |
| Luas Kerucut |
Volume Kerucut
 |
| Volume Kerucut |
Bola
 |
| Bola dalam tabung |
Sebuah Bolah yng dapat masuk kedalam tabung dengan tepat, berarti :
a. diameter bola = diameter tabung
b. tinggi tabung = diameter bola = diameter tabung
Dalam keadaan ini Archimedes merumuskan hubungan berikut.
Luas Permukaan Bola : Luas Permukaan Tabung = 2 : 3
Luas Permukaan Bola
 |
| Luas Permukaan Bola |
Luas Belahan Bola Padat
 |
| Luas Belahan Bola Padat |
Volume Bola
 |
| Volume Bola |
PERUBAHAN VOLUME BANGUN RUANG SISI LENGKUNG
___________JIKA UNSUR-UNSURNYA BERUBAH__________
Besar Perubahan volume tabung jika jari-jarinya berubah
 |
| Perubahan Volume tabung jika jari-jarinya berubah |
Jika tabung dengan jari-jari r diperbesar menjadi tabung berjari-jari R dan tingginya tetap t maka :
Perubahan volume tabung = volume tabung akhir - volume semula
 |
| Perubahan Volume Tabung jika R > r |
Jika tabung dengan jari-jari r diperkecil menjadi tabung berjari-jari R dengan tinggi tetap, maka :
Perubahan volume tabung = volume semula - volume akhir
 |
| Perubahan Volume Tabung jika r > R |
Besar perubahan volume kerucut jika jari-jarinya berubah
 |
| Perubahan Volume Kerucut |
Jika kerucut dengan jari-jari r diperbesar menjadi kerucut berjari-jari R dan tingginya tetap maka :
Perubahan volume kerucut = volume akhir - volume semula
 |
| Perubahan Volume Kerucut jika R > r |
Jika kerucut dengan jari-jari r diperkecil menjadi kerucut berjari-jari R dan tingginya tetap, maka :
Perubahan volume kerucut = volume semula - volume akhir
 |
| Perubahan Volume Kerucut jika r > R |
Besar perubahan volume bola jika jari-jarinya berubah
 |
| Perubahan Volume Bola |
Jika bola dengan jari-jari r diperbesar menjadi bola berjari-jari R, maka :
Perubahan volume bola = volume akhir - volume semula
 |
| Perubahan Volume Bola jika R > r |
Menggunakan cara yang sama, jika bola berjari-jari r diperkecil menjadi bola berjari-jari R, maka :
Perubahan volume bola = volume semula - volume akhir |
| Perubahan Volume Bola jika r > R |
Sekian rangkuman materi untuk materi BANGUN RUANG SISI LENGKUNG, materi ini merupakan materi untuk Sekolah Menengah Pertama Kelas IX semester ganjil.


0 Response to "BANGUN RUANG SISI LENGKUNG Matematika Kelas 9 SMP"
Post a Comment